News + Trends

Vampire tile replaces the "Einstein"

6.6.2023

Translation: machine translated

A single tile from which only non-periodic patterns can be created: The Einstein tile made headlines in March 2023. But now there is a new, even more cleverly shaped tile that also manages without reflections.

In March 2023, a mathematical discovery also made headlines outside the specialist world: New York Times, CNN, Süddeutsche Zeitung and others reported on the 13-sided geometric shape, which reminds some people of a hat and others of a T-shirt. This polygon can be used to cover a plane without gaps - and the resulting pattern is always non-periodic.

A shape that fulfils these two requirements is known as an Einstein tile (the name is derived from "a stone" and has nothing to do with the famous physicist). Mathematicians had been looking for such a tile for decades, and some had already given up hope of finding one. "I was particularly surprised by the simplicity of the shape," says mathematician Michaël Rao from the École normale superieure in Lyon.

An aperiodic monotile.
Source: D. Smith et al.

However, the hat tile presented in spring 2023 had one drawback: in order for it to fill the plane without gaps, reflections of the 13-corner must be allowed. "The big question was whether an Einstein tile exists that doesn't need to be mirrored," explains Rao. Some call such a shape a "vampire tile" because, like the mythical night creature, it has no mirror image. The discoverers of the hat tile, David Smith, Joseph Samuel Myers, Craig S. Kaplan and Chaim Goodman-Strauss, have now presented such a vampire tile in an as-yet-unpeer-reviewed paper on the preprint platform ArXiv.

Once again, it's an amateur mathematician who finds the vampire tile

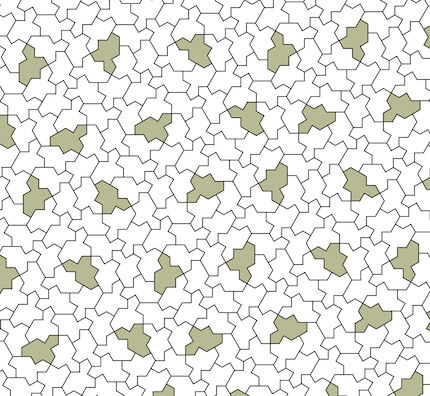
As the team found in their previous publication, by changing the edge lengths of the hat, other tile shapes can be found that also create gapless pavements. When retired printing plant technician David Smith cut one of these tile shapes out of paper and played around with it, he noticed something exciting: When he put the tiles together without mirroring them, a gapless, non-periodic pattern seemed to emerge.

"Naturally, (Joseph Samuel Myers, Chaim Goodman-Strauss and I) began to work more intensively on this form," writes the computer scientist Kaplan on Mastodon. After a few months of work, he and his two colleagues were able to prove their suspicions: The tiling investigated by Smith merely does not allow periodic tiling if you do not allow mirrored parts.

Vampire tile
Source: David Smith, Joseph Samuel Myers, Craig S. Kaplan, Chaim Goodman-Strauss

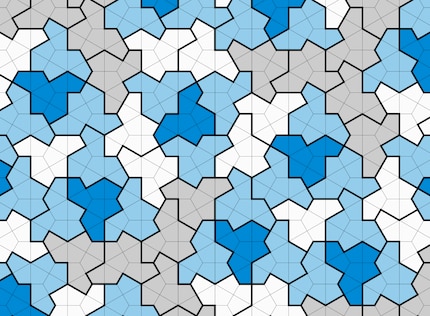
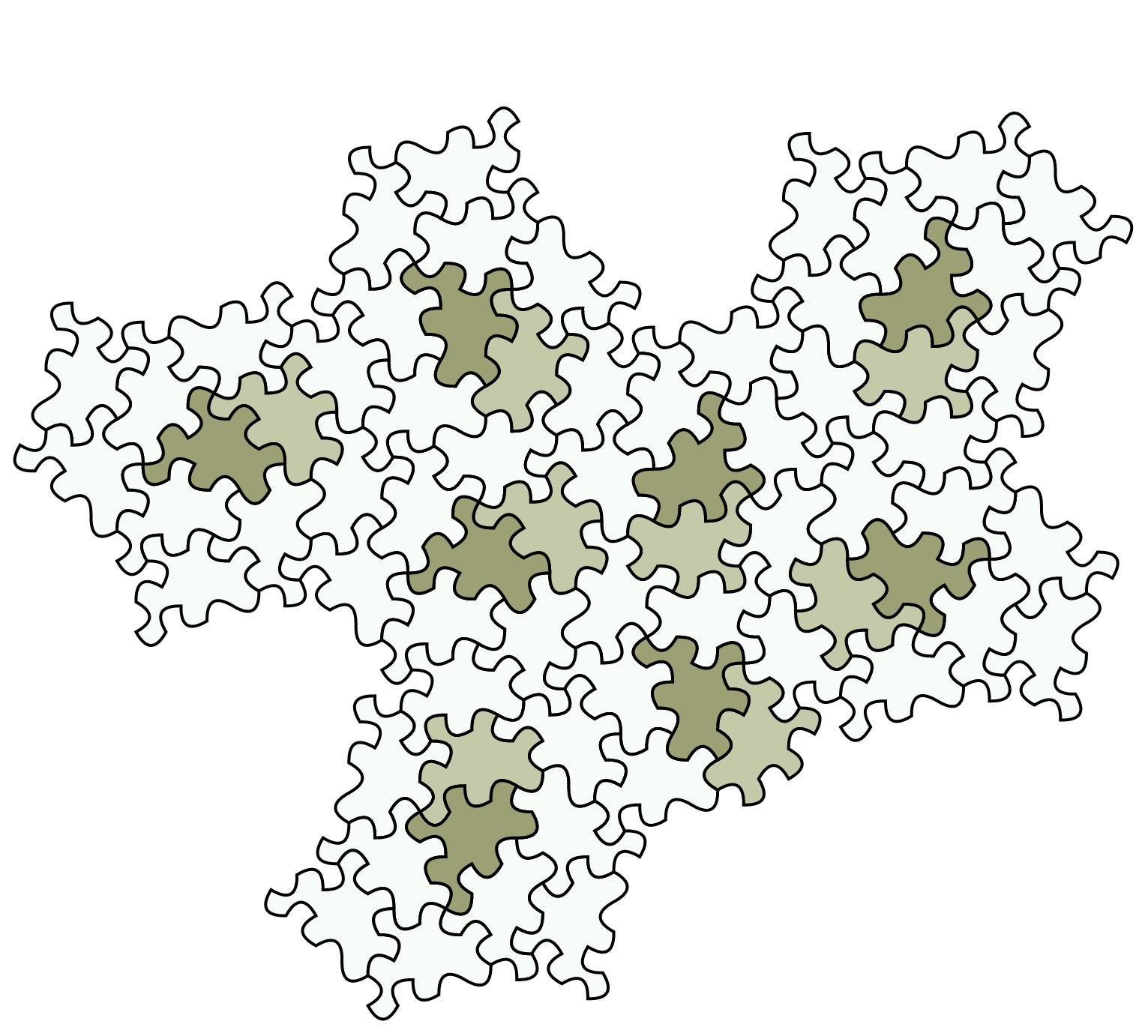
However, the scientists were not entirely satisfied. After all, if mirrored versions of the new tile are inserted, periodic patterns can also be generated. That's why they changed the shape of the 13-sided tile and rounded the corners to create a new tile that looks more like a puzzle piece. This tile, which they call "Spectre", can only cover a plane without gaps if no mirrored versions are allowed. And the patterns generated are inevitably not periodic. According to the researchers, they have thus found a vampire tile: a coherent Einstein that does not need a mirror image in order to pave a plane without gaps and necessarily not periodically.

Because some experts were not happy with the fact that the hat tile presented in March 2023 has to be mirrored. "The problem is not just that it appears mirrored," says mathematician Michael Baake from Bielefeld University, "but that one of the two versions - mirrored or not mirrored - inevitably appears more frequently in a tiling than the other." This problem is related to a special property of aperiodic patterns: Anyone standing on a plane that is tiled in an aperiodic way cannot judge from the pattern which area of the plane they are in or what type of tiling it is - an infinite number of different tiling patterns can be created from one Einstein. However, as there are hat parquet patterns with predominantly mirrored or predominantly non-mirrored tiles, it is at least possible to distinguish between these two variants. However, this contradicts the actual characteristic of aperiodic parquetry, which does not allow any differentiation at all.

The newly discovered Spectre tile, on the other hand, seems to fulfil all the requirements of an Einstein: It is a single continuous tile that is merely rotated and shifted along the plane, creating a gapless, always irregular pattern. And because it does not require any mirroring, it is also easier for tile manufacturers to produce the tiles for a perfect nerd bathroom.

But mathematicians can't rest on their laurels just yet. "It would be interesting to find out how many sides an Einstein tile needs as a minimum," says Rao. "Or whether a purely aperiodic tile can also be a polygon." The new goal is therefore to find the simplest possible Einstein tile. The hunt is on.

Spectrum of science

We are partners of Spektrum der Wissenschaft and want to make well-founded information more accessible to you. Follow Spektrum der Wissenschaft if you like the articles.

[[small:]]

Cover photo: David Smith, Joseph Samuel Myers, Craig S. Kaplan, Chaim Goodman-Strauss

19 people like this article

Spektrum der Wissenschaft

Wissenschaft aus erster Hand

dirdjaja@spektrum.de

Experts from science and research report on the latest findings in their fields – competent, authentic and comprehensible.

News + Trends

From the latest iPhone to the return of 80s fashion. The editorial team will help you make sense of it all.

Show all

Your data. Your choice.

Search

Vampire tile replaces the "Einstein"

Once again, it's an amateur mathematician who finds the vampire tile

Spectrum of science

Comments

Top 10 categories

Go to

Comments

Galaxus Deal of the day