What’s sampling rate got to do with quality of digital music?
15.2.2022
Translation: Veronica Bielawski
At first glance, the sampling rate is a purely a technical specification in the audio world. But understanding how it works will revolutionise your understanding of digital music.
An article on sampling rate? Sounds boring. On the surface, sampling rate seems like nothing more than a dry technical specification. But faced with the question of how sampling rate affects sound quality, I’ve found that I, as well as others, possess quite some half-knowledge and misunderstandings. And this, in turn, is linked to a misconception about the very nature of digital music: that it’s all hacked up – and sounds that way.
The basics
What is the sampling rate anyway? Let’s have a look at the graphical representation of a sound wave. The horizontal x-axis is time. The vertical y-axis is the amplitude, or how loud the signal is. The pitch is determined by wavelength: in a high pitch, the waves are closer together. Put differently: in a high pitch, the oscillation repeats more frequently, so it has a higher frequency.
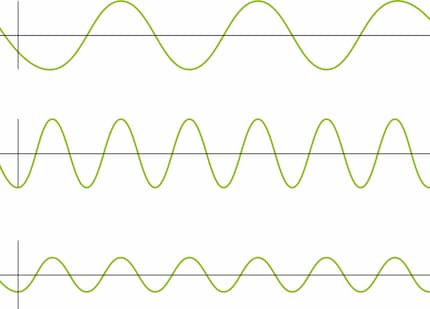
The sampling rate is also represented as a frequency, as it denotes the frequency with which the amplitude is measured on the x-axis. In other words: it’s the frequency with which an audio sample is taken. Hence the term «sampling rate».
The sampling rate is the clearest distinguishing feature between analogue and digital music. Analogue media stores a continuous signal, so there’s no sampling rate. Digital recording methods record sound at specific time intervals.
The misunderstanding
This makes it sounds as if analogue music is superior to digital music on principle; as if digital music is always just an approximation of the analogue original and therefore can never be as good. This is a fallacy.
For one thing, we’re not just comparing analogue and digital here, but original sound and recording. Of course, nothing beats the original. Any recording is at most as good as the original. But this also holds true for analogue recordings. They too come with losses in quality such as noise and distortion. Only direct sound transmission without a medium is truly superior on principle – listening to a live instrument, for example.
The misunderstanding probably stems from the fact that sound waves themselves are analogue. Strictly speaking, there’s no such thing as digital music – only digitally stored music. To record sound, an analogue-to-digital converter is required, which generates digital data from the analogue sound waves. And for playback, a digital-to-analogue converter is required to do the reverse.
The audio signal is always converted. It must be – even with an analogue recording. And during playback, sound must be recreated from the stored medium; a loudspeaker converts an electrical signal into mechanical motion.
Not to mention the fact that recording studios started switching to digital recording as early as in the late 1970s. This means that even when you buy a record, there’s been a conversion from analogue to digital and back to analogue.
But there is an even more common misconception about digital music. And it’s also related to the sampling rate.
Digital doesn’t mean choppy
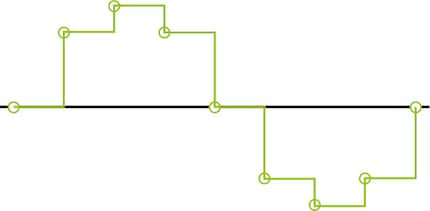
By measuring sound at regular intervals, we get individual points on the sound curve diagram. For playback, these points need to create a complete sound curve. Here’s where many analogue aficionados – mistakenly – assume that the resulting sound curve looks like this:
Or even like this:
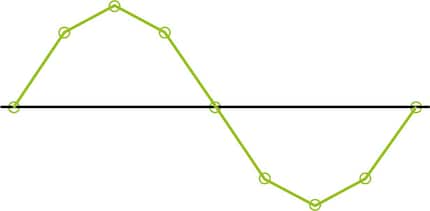
This is, in fact, not the case. The sound curve generated from digital data looks something like what you see below – it’s just as round as an analogue one.
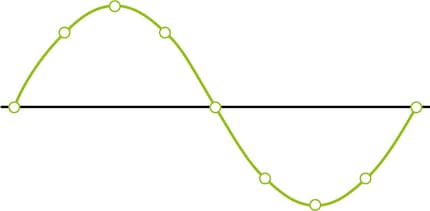
What this means is that the fragmentation of sound into individual data points can be completely reversed when converted back into real sound waves. Black magic? Not quite – mathematics. Curves are mathematical functions. However, they require a minimum number of measuring points – i.e. a minimum sampling rate. And that’s where the Nyquist-Shannon sampling theorem comes in.
The Nyquist-Shannon sampling theorem
The theorem states that if the sampling rate is high enough, a sound curve completely identical to the analogue original can be reconstructed. And it also states how high the sampling rate must be. Namely, twice as high as the highest frequency to be sampled.
Here’s the most common example to illustrate this: an audio CD has a sampling rate of 44,100 Hz, or 44.1 kHz. That means there are 44,100 samples per second. According to the Nyquist theorem, this allows frequencies of up to 22,050 Hz to be perfectly reconstructed. This should be more than enough, because no human can hear a frequency higher than that, anyway. Most adults can’t hear anything above 15,000 Hz.
However, the theorem only holds true if one important restriction is met: all frequencies above 22,050 Hz must be filtered out. You can see this in the diagram below. The black dots are the samples. There are two curves of different frequencies that fit into these samples. This being the case, it’s unclear which of the two is the correct frequency.
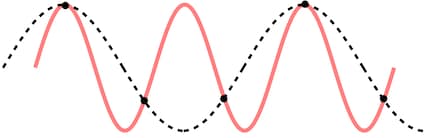
But the red curve has a higher frequency than the dotted black curve. If the frequency of the red curve is higher than half of the sampling rate, it gets filtered out and we end up with a unique curve.
This is no coincidence. It’s not possible to draw a curve with a lower frequency than the red one which also fits the sample points. This is precisely what the Nyquist-Shannon theorem states.
Oversampling
The Nyquist theorem itself is considered beyond dispute. So why are there digital-to-analogue converters that have several times the CD sampling rate? Is it overkill? Rabble-rousing, even?
Not necessarily. Here’s the crux of the matter: the Nyquist theorem only states that the high frequencies must be filtered out. It doesn’t say anything about how this should be done. In fact, to this day it’s not possible to perfectly filter out everything above a specific frequency.
At a sampling rate of 44.1 kHz, a low-pass filter is needed that filters both as little as possible up to 20 kHz, as well as everything above 22.05 kHz. This leaves a very narrow frequency range as a transition. If the signal isn’t filtered perfectly, the sound wave may be mirrored to the left, creating a kind of pre-echo.
At a high sampling rate, this transition range increases, allowing the effect to be better avoided. In recording studios, high sampling rates have been the norm for a long time. For playback, on the other hand, they’re relatively new.
In a nutshell
The fact that digital music consists of individual samples instead of a single, continuous one isn’t a disadvantage. The samples can be used to reconstruct sound waves in a manner indistinguishable from the original. In theory, the only requirement is that the sampling rate is twice as high as the highest frequency of what you’re recording. In practice, this doesn’t actually result in a flawless reconstruction of sound, because no perfect low-pass filters exist. And it is true that recording and playback devices can filter better when fed with a higher sampling rate.
The real question is whether the difference is audible. Even among experts, opinions differ. It’s clear that 44.1 kHz and 48 kHz also provide good quality. If the sound is bad, it could be due to anything – from the recording itself to the speakers. If – and only if – everything else is perfect, then perhaps the sampling rate has something to do with the issue.
David Lee
Senior Editor
David.Lee@digitecgalaxus.chMy interest in IT and writing landed me in tech journalism early on (2000). I want to know how we can use technology without being used. Outside of the office, I’m a keen musician who makes up for lacking talent with excessive enthusiasm.
